Advent of Code 2018, Day 23

For the last three years, Eric Wastl has celebrated the holidays by releasing the Advent of Code, which is a series of 25 holiday-themed coding challenges. They start simple, but by the end they're pretty damned interesting. I highly recommend giving the series a shot. Rather than going over the solution to every day, I want to talk about my favorite puzzle: Day 23.

The challenge

You're given a list of coordinates representing a cloud of drones in 3D space, and each drone has a variable signal signal strength represented by the radius in which a drone can communicate. Your job is to find the point in the cloud where you can communicate with the most drones. The input looks something like this, with 1000 distinct drones in the list:

pos=<-13227272,16297847,20713224>, r=74781821
pos=<-13506391,-11400225,79194067>, r=98387056
pos=<51916866,7859874,63870681>, r=67604198
pos=<6053871,-6125982,40030492>, r=58607212

A couple of things jump out. First, the ranges are HUGE. The search area will be gigantic. Second, the signal strength of each drone is ALSO very large; we're going to see a ton of overlap. Here we see the drones represented with and without their signals. (For the rest of the images I'm going to hide the radius, because it's visually noisy.)

An initial failure

The first thing I tried is starting in the middle of the cloud of drones, searching near that point to find the point with the most drones, then repeating from that new point. My implementation was to throw out a big sphere, pick the best point, throw out a slightly smaller sphere from that new point, and repeat until we'd converged on an area with a lot of drones. (Why a sphere? Well, because it sounded cool. I ended up tossing it for a cube.) This solution sort of worked, but it ended up getting stuck in local maxima that it was unable to escape. This is a similar to problems of gradient descent; the algorithm can settle into a low point, but not the lowest point.

Here's an abbreviated version of that first attempt:

def most_central_location(self):

   step_size = 10000000
   mean_point = (avg_x, avg_y, avg_z)
   best_point = mean_point
   most_bots, best_dist = point_score(mean_point)

   while step_size >= 1:
       points = points_on_sphere(100, best_point, step_size)

       for point in points:
           bots, avg_dist = point_score(point)  # avg_dist ignores signal strength 

           if bots > most_bots or bots == most_bots and avg_dist < best_dist:
               best_point = point
               most_bots = bots
               best_dist = avg_dist

       step_size //= 2

   return best_point

A working answer

Clearly we need to be able to path through areas with fewer drones if the right path is on the other side. It's too optimistic to assume that you can just cleanly walk from your starting point towards the neighboring areas with the most drones. In order to fix this we need a way to track a number of different potential areas, and resume our search from the one we think is most promising. Enter the heap! We'll pop things off of the heap in the order of how good we think they might be. We want a couple of things from our search areas; we want a lot of drones, and we want a small search area.

Here is the core of the working algorithm:

def most_central_location(self):

    mean_point = (avg_x, avg_y, avg_z)
    search_area = SearchArea(
        center=mean_point,
        bots_in_range=self.bots_in_range(mean_point, size),
        search_size=size)

    heap = [search_area]

    while heap:
        area: SearchArea = heappop(heap)
        if area.search_size == 0:
            return area

        points = BotSwarm.octants(area.search_size, area.center)

        for point in points:
            bots = self.bots_in_range(point, area.search_size // 2)
            new_area = SearchArea(center=point,
                                  bots_in_range=bots,
                                  search_size=area.search_size // 2)

            heappush(heap, new_area)

    return None

Okay, perfect, this works for the puzzle input! Let's watch it in action.

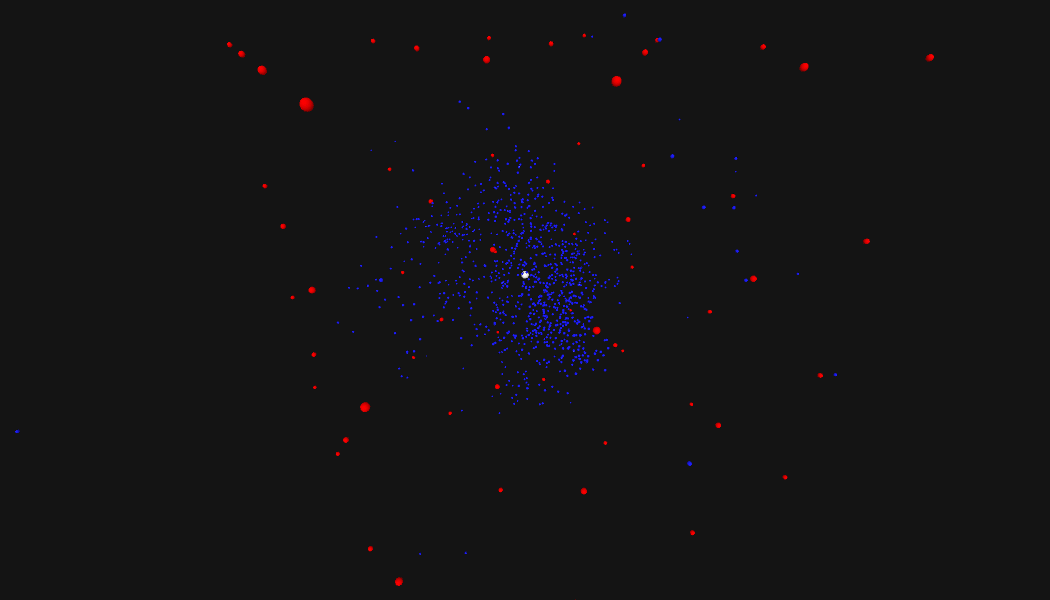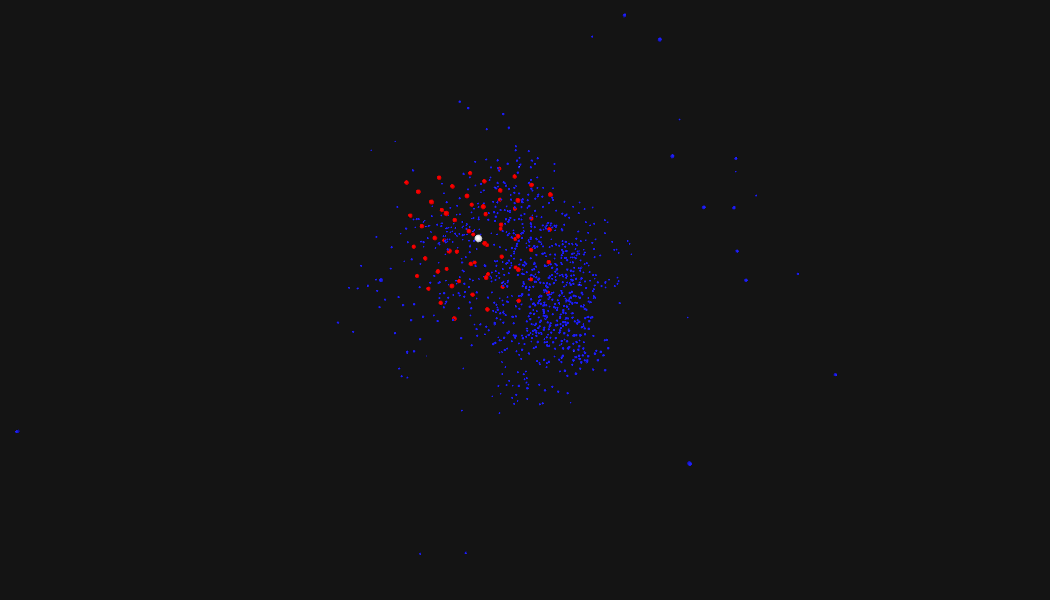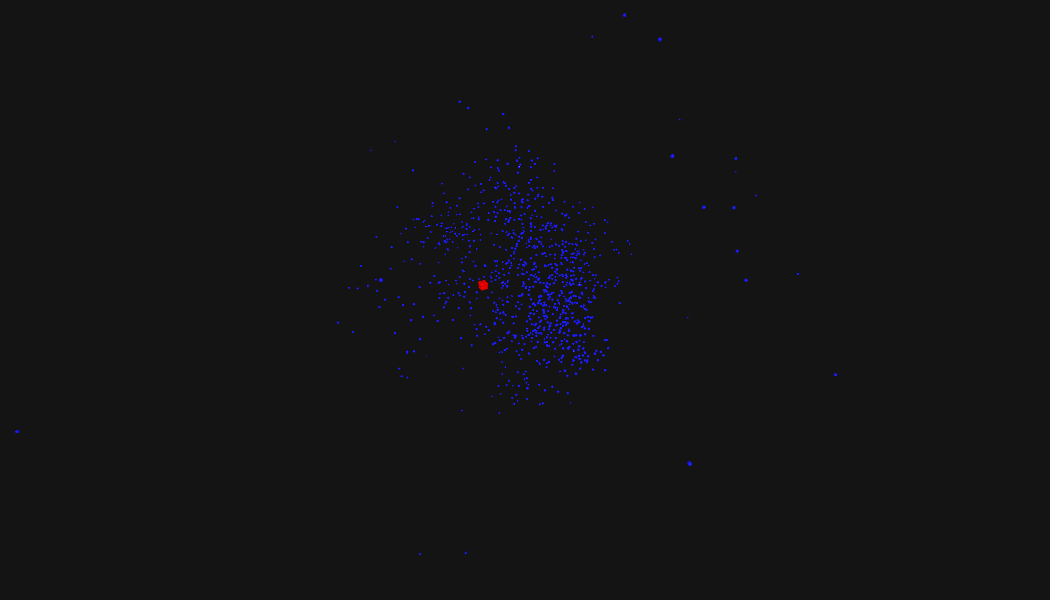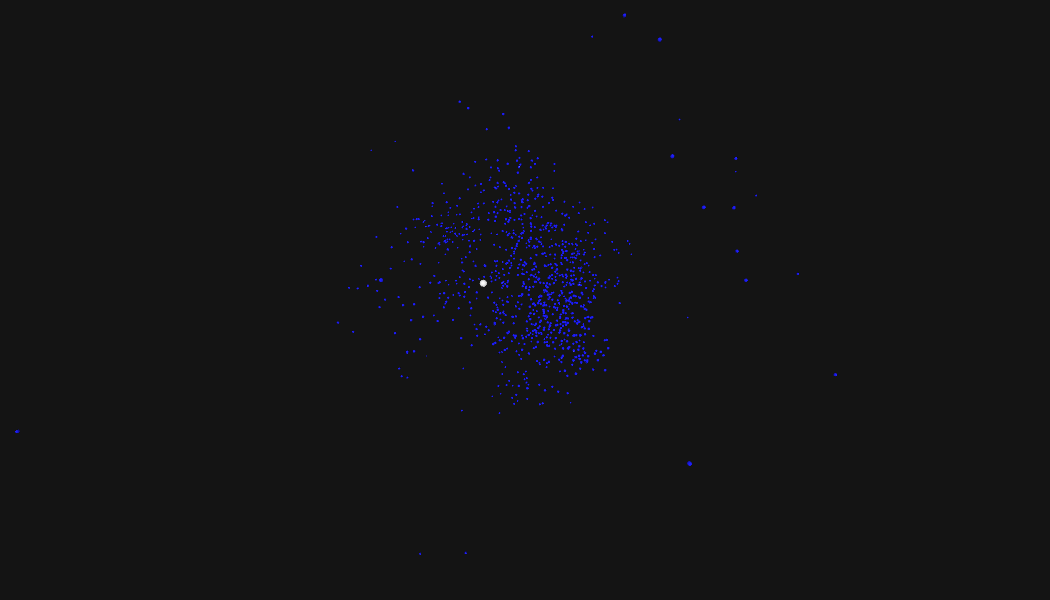
Adversarial Input

So, will our algorithm work for all problems of this type? It will not! Someone created a neat adversarial input for this puzzle, and it causes my solution to take an unreasonable amount of time. Let's check it out.

pos=<1000000,-1000000,0>, r=1499999
pos=<1500000,-1500000,0>, r=1499999
pos=<2000000,-2000000,0>, r=1499999
pos=<2500000,-2500000,0>, r=1499999

Uh oh. This looks like evenly spaced points with an identical radius for every drone. Every search area is going to be nearly identical. Lets watch the algorithm choke:

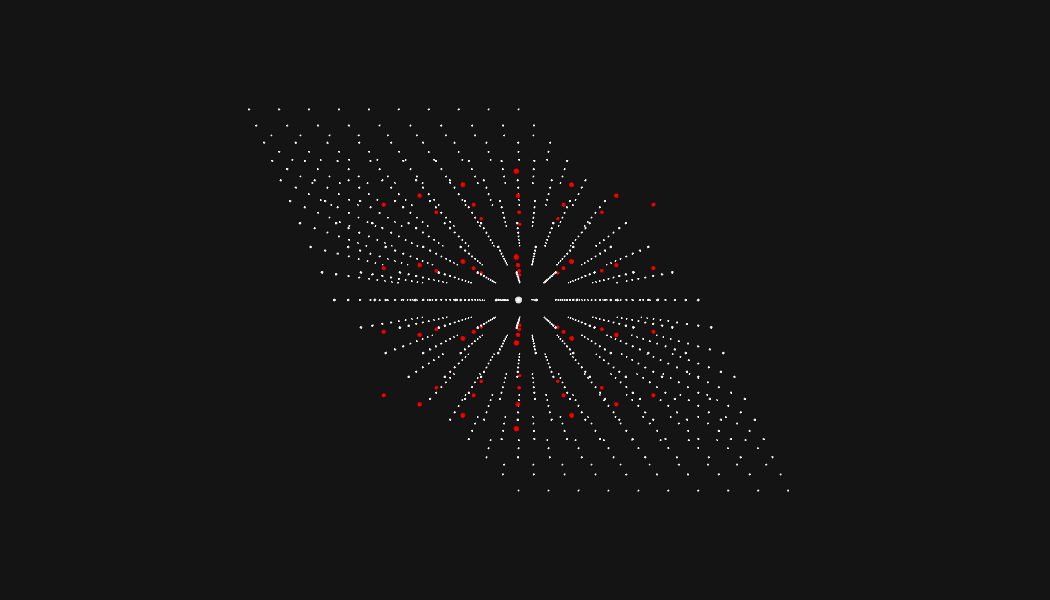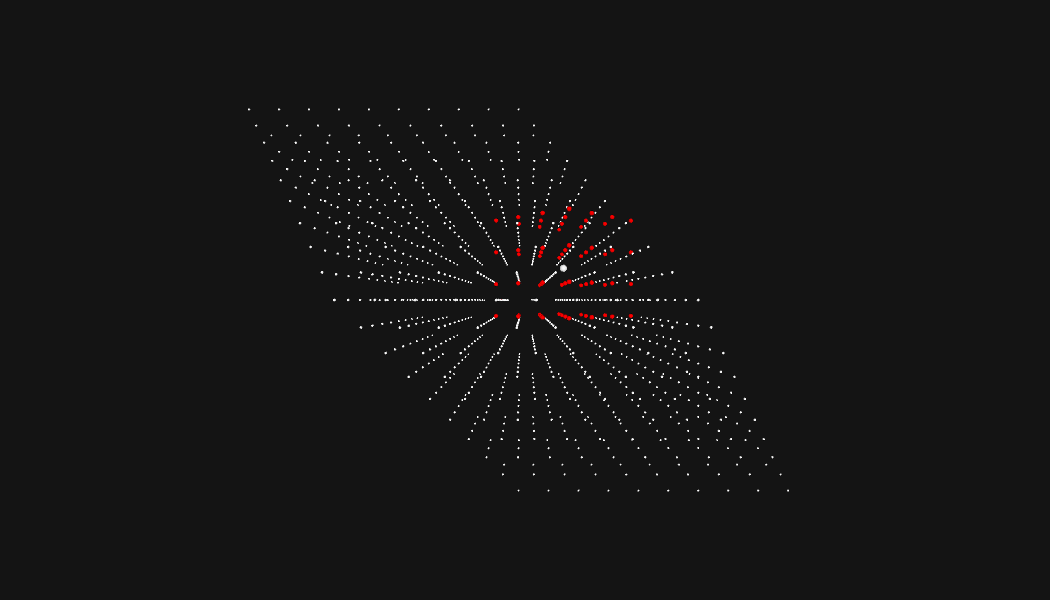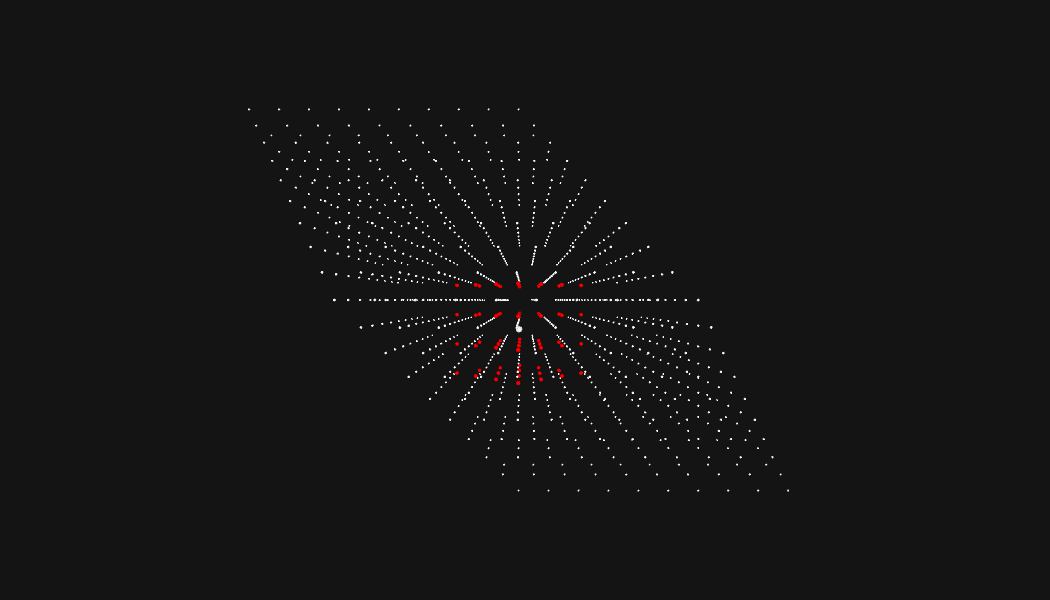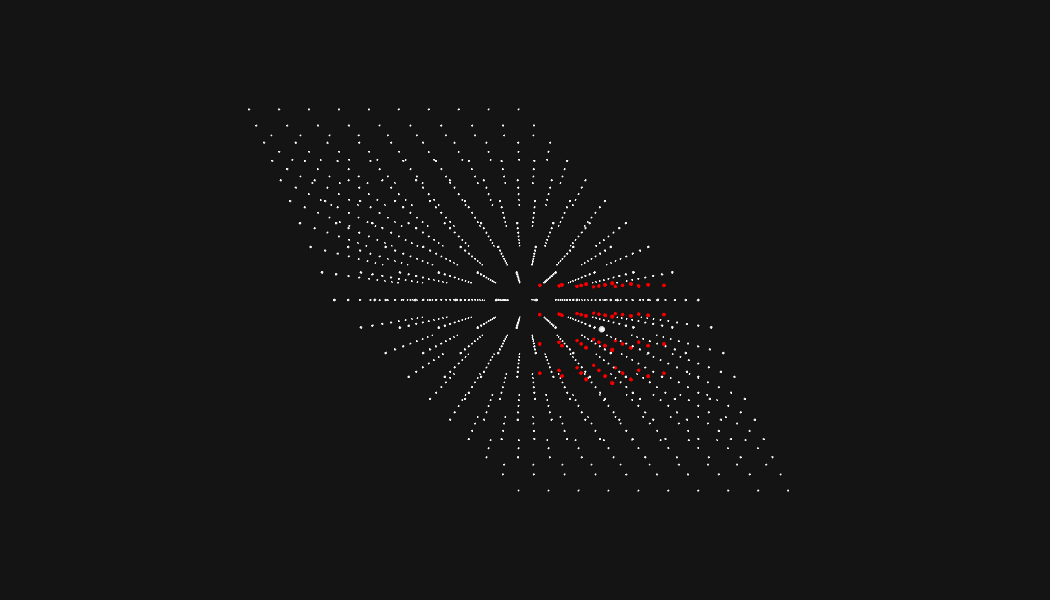
Welp. As you can see, Eric was nice enough that the bot formation he chose for the problem was solvable in a reasonable time with this kind of pathfinding type approach.

Other Solutions

The Advent of Code subreddit thread on Day 23 was full of great discussion. Many people solved this problem with a solution similar to the one I used, and some used other techniques.

Z3 SMT Solver

A popular path was to use the Z3 SMT solver, and if you have no idea what that is then we're on the same page. My fuzzy understanding after a quick read is that you give it constraints and a pile of data, and it tells you if the data can satisfy those constraints.

4D Coordinates

Another person (github.com/fizbin) directly attacked the adversarial input by translating the 3D points into 4D coordinates. I'll leave digging into those solutions as an exercise for the reader!

Full code

You can check out my full code for Day 23 here, along with my solutions for the other 25 days on Github.